Ohm’s Law Calculator
Ohms law calculator is an online tool that calculates the following quantities in a circuit.
• Resistance
• Voltage
• Current
If two values are known, third value can be found using this resistance calculator.
In this post, we will discuss Ohm's Law, its formula, how to find current, voltage, and resistance without using vape coil calculator.
How to use ohms law calculator?
To use ohm's law calculator, follow the steps below.
• Enter the resistance and current to calculate voltage.
• Enter the resistance and voltage to calculate current.
• Enter the voltage and current to calculate resistance.
You don’t need to press any button to find voltage using vape ohm calculator because it calculates the values in real-time.
What is Ohm's Law?
Ohm's Law is one of the most basic and important electric and electronic circuit laws.
Ohm's Law states that the current flowing into a circuit is directly proportional to the potential difference and inversely proportional to the circuit resistance. Ohm's Law symbol is denoted by Ω letter.
Ohm's Law Equation
Ohm’s law formula can be mathematically expressed:
V = IR
In this equation:
V = Voltage expressed in Volts
I = Current expressed in Amps
R = Resistance expressed in Ohms
Ohm's law triangle
In order to keep in mind the formulas, a triangular shape can be used to represent voltage, resistance, and current formula. This is sometimes referred to as the Ohm's Law triangle.
Cover the unknown quantity and evaluate the equation using the remaining quantities.
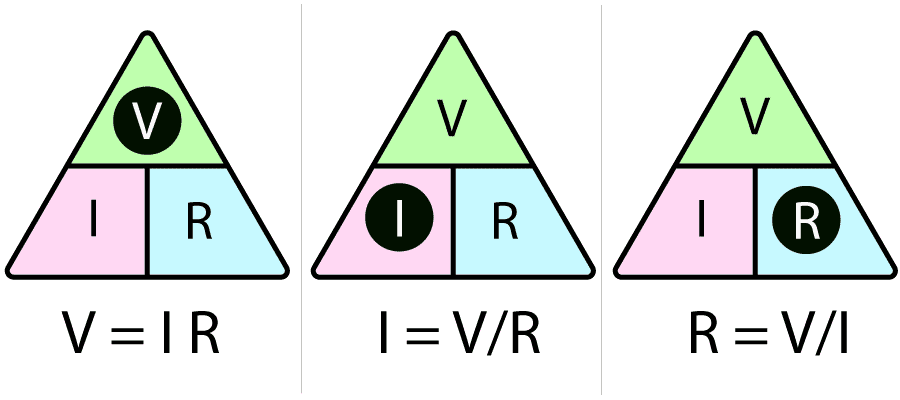
Ohm's Law Wheel
The Ohm’s Law chart below represents the relationship between P, R, V, and I in Ohm's Law.
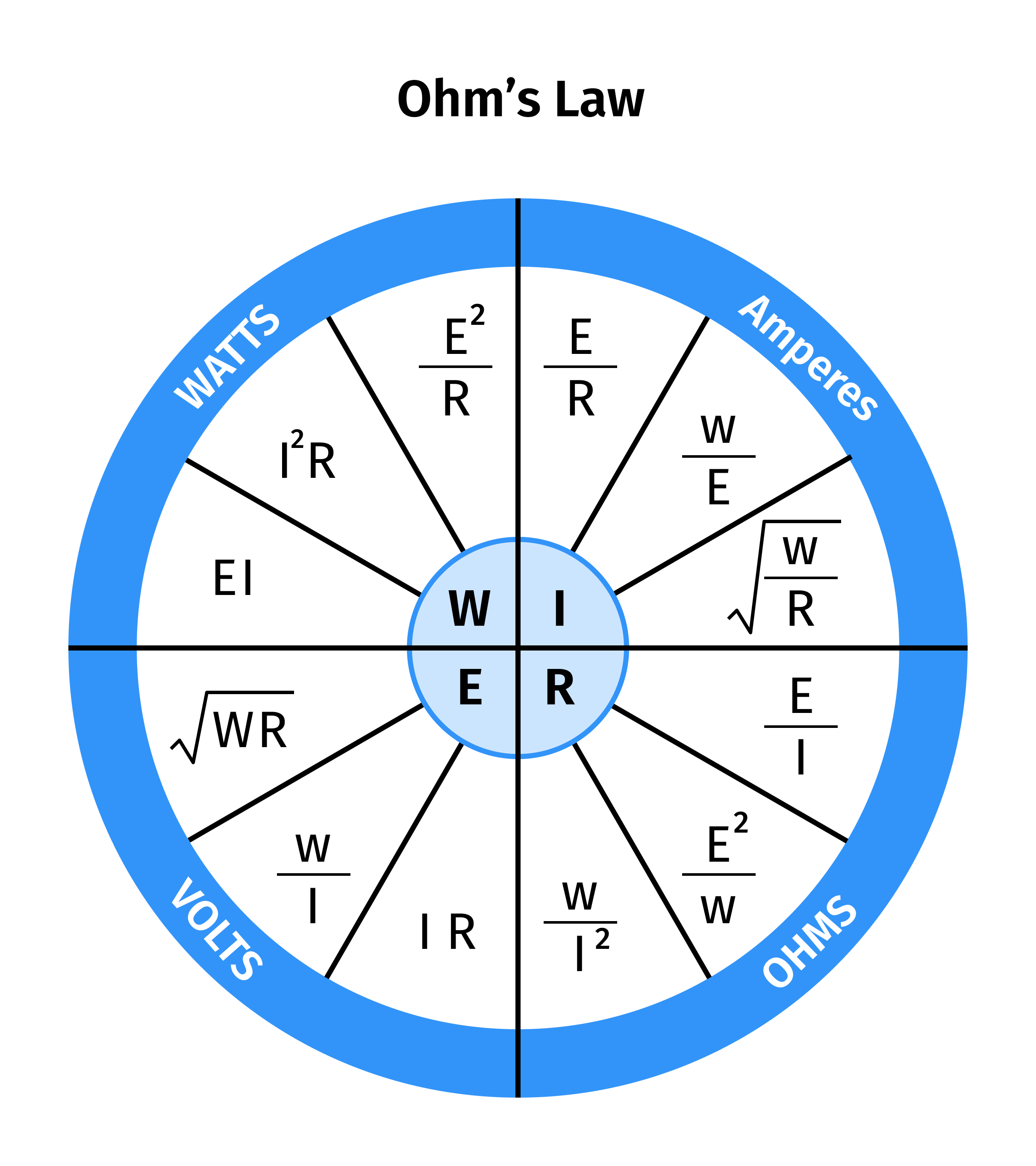
How to calculate voltage?
Wondering what is voltage? Voltage is the product of current and resistance.
The Ohm's Law serves as an algebraic formula for measuring the voltage (potential difference) in the presence of resistance and current.
Example:
Suppose there is 2 ampere of current and 200-ohm resistance in a wire. Calculate the voltage by using these two quantities?
Solution:
Step 1: First of all, identify the values.
I = 2 Amp
R = 200 ohm
Step 2: Write down the Ohm's equation.
V = IR
Step 3: Substitute values in the equation and solve.
V = 2 × 200 = 400
V = 400 volts
How to calculate resistance?
Example:
Suppose there are 3.5 amperes current and 32 volts in a circuit. Calculate the resistance by using the given quantities?
Solution:
Step 1: We will identify values first.
I = 3.5 Amp
V = 32 volts
Step 2: Write down the Ohm's equation.
V = IR
Step 3: Substitute values in the resistance formula.
V = IR , R = V/I
R = 32/3.5
R = 9.14 Ω
How to calculate current?
Example:
Calculate the current in amps if there is 20 ohms of resistance and 40 volts of potential difference in a circuit.
Step 1: Write down and identify the values.
R = 20 ohms
V = 40 volts
Step 2: Write down the equation of Ohm’s law.
V = IR
Step 3: Place the values in the equation.
V=IR, I=V/R
I = 40/20
I = 2 amperes
Use the vape coil calculator above to verify the answers in these calculations.