Circumcenter Calculator

In this post, we will define circumcenter, discuss how to find circumcenter, and how to use our calculator to find circumcenter.

What is Circumcenter?

Many people think that circumcenter and centroid are the same points. But it is a mistake!

The circumcenter is the point at which the perpendicular bisectors of a triangle cross each other. It lies outside for an obtuse, at the center of the Hypotenuse for the right triangle, and inside for an acute.

The bisectors are nothing more than the ray or thread, which splits a line into two equal parts 90 degrees. The longer side of the right-angle triangle is Hypotenuse.

For example, in the picture, O is the circumcenter of triangle ABC.

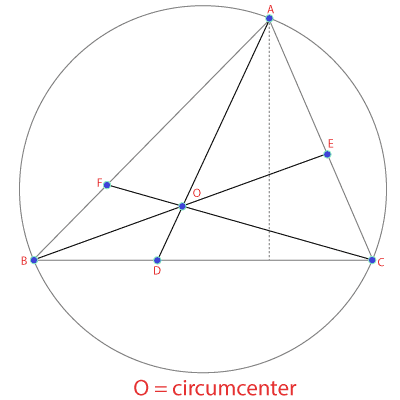
Need to calculate the area of the triangle before calculating the circumcenter? Use our triangle area calculator.

How to find the circumcenter of a triangle?

Assume the points of the sides of a triangle are \(A (4, 5), B (6, 8),\) and \(C (3,-2)\). Consider x1, y1, and x2, y2 as the points on the sides of the triangle, respectively.

To find the points of the circumcenter, we need to define the equation of the perpendicular bisector. Follow the below steps to find the circumcenter of a triangle:

Step 1: First of all, calculate the midpoint of the combined x and y coordinates of the sides AB, BC, and CA.

Midpoint = \(\dfrac{(x_1+x_2)}{2}\) and \(\dfrac{(y_1+y_2)}{2}\)

Place corresponding values in above equation to calculate midpoints for each line separately.

Midpoint of AB = \(\dfrac{(4+6)}{2}, \dfrac{(5+8)}{2} = (5, \dfrac{13}{2})\) 

Midpoint of BC = \(\dfrac{(6+3)}{2}, \dfrac{(8-2)}{2} = (\dfrac{9}{2}, 3)\)

Midpoint of CA = \(\dfrac{(3+4)}{2}, -\dfrac{2+5}{2} = (\dfrac{7}{2}, \dfrac{3}{2})\)

Step 2: The slope on the AB, BC and CA sides must be found with the formula \(\dfrac{(y_2-y_1)}{(x_2-x_1)}\). The letter m is used to represents the slope.

AB (m) = \(\dfrac{8-5}{6-4} = \dfrac{3}{2}\)

BC (m) = \(\dfrac{-2-8}{3-6} = \dfrac{10}{3}\)

CA (m) = \(\dfrac{-2-5}{3-4} = 7\)

Step 3: In this step, we will measure the slope of the AB, BC and CA perpendicular bisector.

(The slope of the perpendicular bisector = -1/slope of the line)

Slope of the perpendicular bisector of AB = \(\dfrac{-1}{(3/2)} = \dfrac{-2}{3}\)

Slope of the perpendicular bisector of BC = \(\dfrac{-1}{(10/3)} = \dfrac{-3}{10}\)

Slope of the perpendicular bisector of CA = \(\dfrac{-1}{7}\)

Step 4: We have to find the equation of perpendicular bisector in this step. We will repeat this step to find equation of perpendicular bisector for each line. To find circumcenter equation, use the formula below:

\(y - y_1 = m(x - x_1)\)

Equation for AB

\(y - y_1 = m(x - x_1) \Rightarrow y - \dfrac{13}{2}= \dfrac{3}{2} \cdot (x - 5)\)

\(2y + 3x = 28\)

Equation for BC

\(y - y_1 = m(x - x_1) \Rightarrow y - 3 = \dfrac{10}{3} \cdot (x - \dfrac{9}{2})\)

\(3y + 10x = 144\)

Equation for CA

\(y - y_1 = m(x - x_1) \Rightarrow y - \dfrac{3}{2} = 7(x - \dfrac{7}{2})\)

\(y - 7x = -23\)

Step 5: Solve any two of the equation from above to find the value of x and y. In this case, after solving two equations, we get \((14.95, -0.136)\) as coordinates of the circumcenter of the triangle.

This is a long process which is why it is suggested to use the circumcenter finder above.