What is Midpoint?
The midpoint of a line or segment is a point that bisects the line in two equal parts. The midpoint is exactly at an equal distance from both endpoints. The term midpoint is a mathematical term related to coordinate geometry.
Midpoint Formula
The equation for the midpoint is
Midpoint =\(\dfrac{X_1+X_2}{2},\dfrac{Y_1+Y_2}{2}\)
You can use this midpoint calculator to auto-calculate the equation and quickly find the midpoint between two points with a step-by-step solution.
How to Find the Midpoint?
Example:
How to find the midpoint of a line segment that is between two points; \(A(4, 2)\) and \(B(6, 4)\).
Solution:
The following formula would be applied.
Midpoint = \(\dfrac{X_1+X_2}{2},\dfrac{Y_1+Y_2}{2}\)
In the above set of points, the values are:
\(X_1 = 4, X_2 = 6, Y_1 = 2, Y_2 = 4\)
Thus, the midpoint would be given as
Midpoint \(= \dfrac{4+6}{2},\dfrac{2+4}{2}\)
Midpoint \(= (5,3)\)
How to Find the Midpoint of a Line Segment?
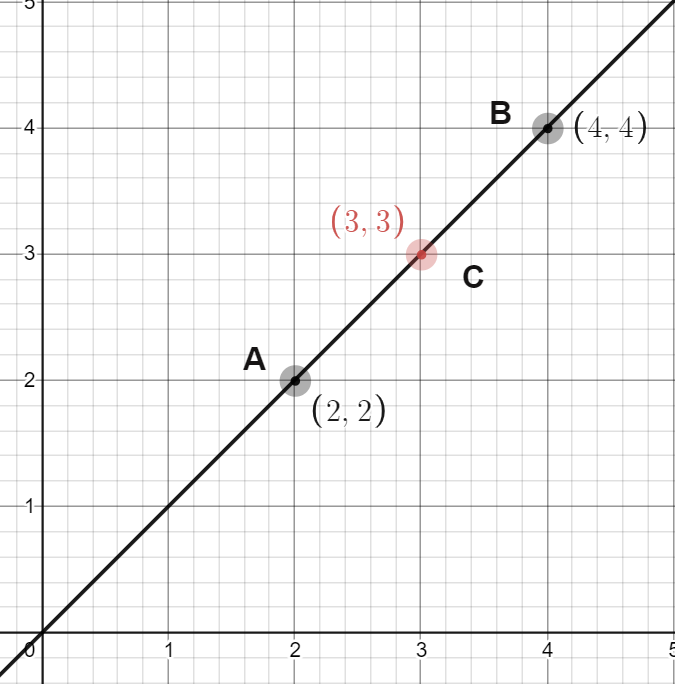
A line is constructed between two sets of points as the diagram shows below.
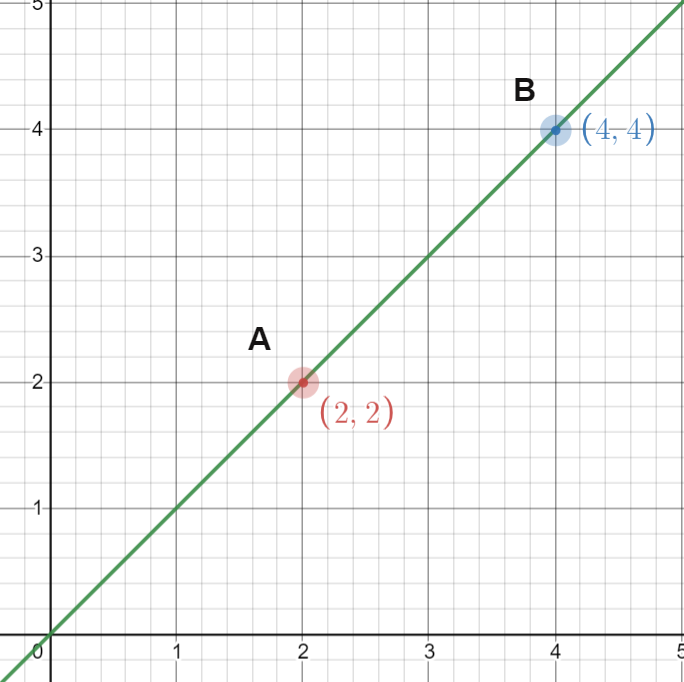
In the above diagram, we can see a line AB where the coordinates are \(A(2, 2)\) and \(B(4, 4)\).
When you talk about the midpoint of AB, it would be present between points A and B. In other words, midpoint coordinates are calculated by taking the average of both points (separately for X and Y).
Consider that the midpoint is C. Thus, C would be given as
\(C =\dfrac{2 + 4}{2} , \dfrac{2 + 4}{2}\)
\(C = (3, 3)\)
As C is the midpoint of line AB;
Midpoint of AB \(= (3,3)\)