Results
Calculate all three quartiles (upper, middle, and lower) as well as the interquartile range (iqr) for the given data set using the quartile calculator.
Along with the quartile values, this calculator also provides a box graph, ascending descending arrangement of values, and median of the group.
How to use the Quartile Calculator?
To use this calculator, follow the steps given below:
- Enter the data set as a quartile range in the given input box. Separate each value using a comma.
- Press the Calculate button to see the results.
It will give you the calculated IQR, first quartile, second quartile, and third quartile.
Give your feedback!
| 1 | What is a quartile? |
| 2 | Quartile formula |
| 3 | How to calculate quartiles? |
Quartile calculator is used to find the first, second, third, and inter quartiles of the given numbers. This q1 q2 q3 calculator also calculates the ascending and descending orders of the given list of numbers.
What is a quartile?
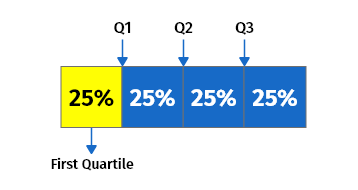
A quartile is a type of quantile that has three points separated into four equivalent classes, each of which accounts for a fourth of the dispersed population.
There is a total of three quartiles in a data set:
1. The first quartile (Q1)
The first quartile also referred to as the lower quartile, is equal to the 25th percentile of the data. The Q1 separates the lowest 25% of data from the highest 75%.
2. The second quartile (Q2)
The second quartile, also known as the middle quartile or median of a data set is equal to the 50th percentile of the data. It cuts data in half.
3. The third quartile (Q3)
The third quartile, also known as the upper quartile (QU), represents the 75th percentile of the data. It separates the lowest 75% of data from the highest 25%.
Quartile formula
The formula for various quartiles can be written as follow:
The Quartile Formula for Q1
The quartile formula for Q1 or first quartile formula can be expressed as:
Q1= \(\dfrac{1(n+1)^{th}}{4}\) term
The Quartile Formula for Q3
The quartile formula for Q3 or third quartile formula can be expressed as:
Q3= \(\dfrac{3(n+1)^{th}}{4}\) term
The Quartile Formula for Q2
The quartile formula for Q3 or third quartile or median formula can be expressed as:
Q2 = \(\dfrac{(n+1)^{th}}{2}\) term
Interquartile Range (IQR)
The quartile formula for interquartile range IQR can be expressed as:
IQR = Q3 – Q1
How to calculate quartiles?
Example
Find all the quartiles for the group below:
\(2, 4, 3, 7, 8, 1, 10\)
Solution
Step 1: Arrange the data in ascending order.
\(1, 2, 3, 4, 7, 8, 10\)
Step 2: Find the first Quartile (Q1):
Q1= \(\dfrac{1(n+1)^{th}}{4}\) term
Q1= \(\dfrac{1(7+1)^{th}}{4}\) term
Q1= \(\dfrac{8}{4}^{th}\) term
Q1= \(2^{nd}\) term which is 2.
Step 3: Find the second Quartile (Q2):
Q2= \(\dfrac{2(n+1)^{th}}{4}\) term
Q2= \(\dfrac{2(7+1)^{th}}{4}\) term
Q2= \(\dfrac{16}{4}^{th}\) term
Q2= \(4^{th}\) term which is 4.
Step 4: Find the third Quartile (Q3):
Q3= \(\dfrac{3(n+1)^{th}}{4}\) term
Q3= \(\dfrac{3(7+1)^{th}}{4}\) term
Q3= \(\dfrac{24}{4}^{th}\) term
Q3= \(6^{th}\) term which is 8.
-
Total Reviews 0
-
Overall Rating
0/5
- Stars
Thank You! For Your Review
Your Review Will Appear Soon.