How to Find the Area of a triangle having three side
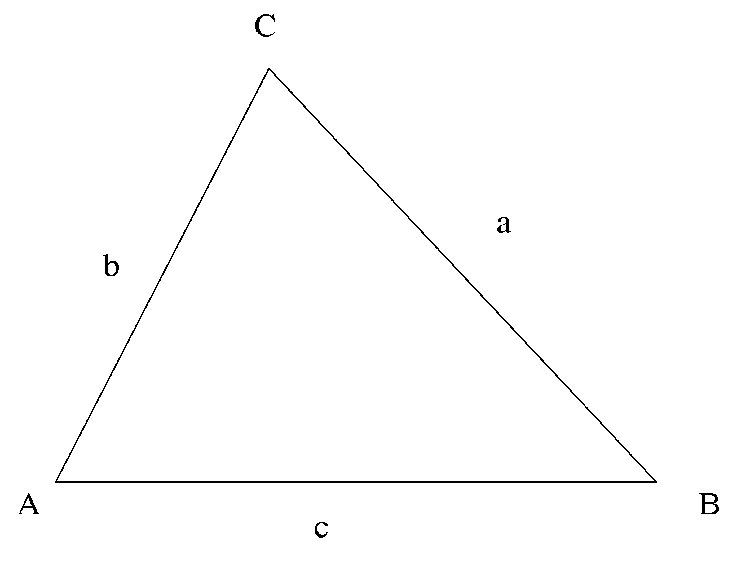
A triangle is a basic and well-known polygon diagram in geometry that has three sides ( a, b and c ) and 3 vertices ( A, B, and C ).
What is the area of a triangle?
The total region surrounded by the three sides of any specific triangle is known as the area of a triangle. There are different formulas to find the triangle area, used according to the known and unknown sides.
When base and height are known: Area of triangle = ½ × b × h
(SSS): Area = 0.25 × √ ((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))
SAS: Area = 0.5 × a × b × sin (γ)
ASA: Area = a² × sin (β) × sin (γ) / (2 × sin (β + γ))
We’re going to discuss the example to understand how to find the area of a triangle.
Example :
Calculate the area of a triangle having three sides of 7 cm, 5 cm, and 11 cm respectively.
Solution:
Because we have all three sides of a triangle, we will use the SSS formula (Heron’s formula) given above.
Step 1: Identify and write down the given values.
a = 7 cm, b = 5 cm, c = 11 cm
Step 2: Write down the triangle area heron’s formula.
Area = 0.25 × √ ((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))
Step 3: Substitute the given values and calculate the area.
Area = 0.25 × √ ((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))
Area = 0.25 × √ ((7 + 5 + 11) × (-7 + 5 + 11) × (7 - 5 + 11) × (7 + 5 - 11))
Area = 0.25 × √ ((23) × (9) × (13) × (1))
Area = 0.25 × √ (2691)
Area = 12.97 cm2
So, the area of a triangle with three sides of 7 cm, 5 cm, and 11 cm is 12.97 cm2.